Copyright © 2006-2022 高顿教育, All Rights Reserved. 网站地图
请问二道三是怎么来的
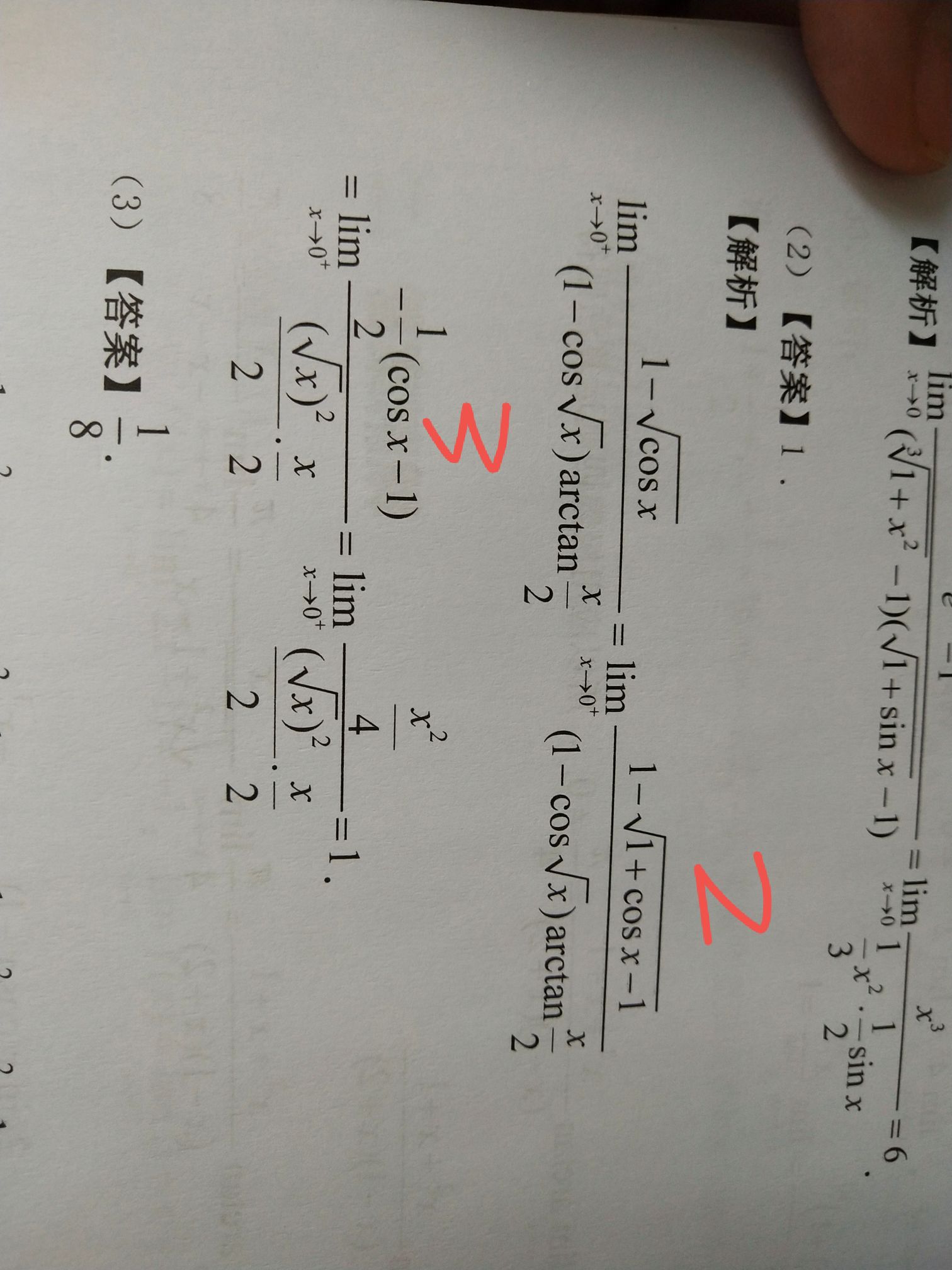
 c同学
c同学用了等价无穷小,把cosx-1看做一个整体。

老师你好,翻译这句的时候为什么for example的例如能...
答案2中逗号前面的部分是个从句还是只是过去分词做状语的形式?...
老师,花销比例可以写成the cost ratio吗?...
判断if是引导条件状语从句还是宾语从句是不是要看if表达的意...
老师,我想买一本单词书,红宝书还是绿皮书好一些?...
upon the same sort of associat...
从a problem 以后怎么翻译呢?这个句子的结构看不懂,...
老师,为什么我觉得这句话这么别扭,感觉看不懂翻译后的解释。“...
老师在宾语从句中,从句充当的是宾语成分吗...
“信中说”放在中间,靠什么来判断前面的部分也是信中的内容呢?...

2023云南艺术学院考研科目已公布!对云南艺术学院感兴趣的同学们快来看看高顿小编整理的2023云南艺术学院考研科目的内容吧!希望对大家起到一定的参考作用。

2023云南师范大学考研招生专业目录已发布!其中特殊教育考研考试科目是什么呢?关于这个问题的答案,高顿小编已经整理好了以下有关内容,感兴趣的同学们赶紧来看看吧!

一个专业会分不同的研究方向或者不区分研究方向,那么云南师范大学美术学专业有哪些研究方向呢?别担心,高顿小编已经整理好了2023云南师范大学美术学考研专业研究方向的相关内容,感兴趣的同学们快来看看吧!

食品科学学硕与食品工程专硕是云南农业大学食品科学技术学院的两个硕士研究生专业,它们的考研科目分别是什么呢?快来一起看看高顿小编整理的2023云南农业大学食品科学与食品工程考研科目的有关内容吧!

2023云南农业大学考研招生专业目录已发布!想要报考云南农业大学的同学们,一起来看看高顿小编整理的2023云南农业大学考研招生专业目录的详细信息吧!里面包含了初试、复试及同等学力考生加试科目。
教师回复: 是这么理解的:正项级数收敛就意味着它们加起来是等于一个常数的,而偶(奇)数项只是正项级数的一部分,那么它们加起来肯定也是一个常数,所以是收敛的。严格的证明需要按照正项级数收敛的定义,用单调有界定理来证明。
教师回复: 可以按照这个来理解因为AB=0,所以矩阵B的列向量都是线性方程组AX=0的解;则矩阵B的列向量组的秩,不大于方程组AX=0的基础解系的个数,也就是说矩阵B的列向量组可以由AX=0 的基础解系线性表示,所以R(B) <= n-R(A),故R(A)+R(B)小于等于n。
教师回复: 这里应该套用的是ln1+x的公式,因为x趋于0的,然后可以把-x带入
教师回复: 这是个感叹句,使用了倒装,顺过来说是 a day makes a difference. 某一天产生了重要的作用/ 某一天发生了一个变化。 用感叹语气,则是 某一天产生了多么大变化啊!(某一天和平时非常不一样);翻译则调整表达为: 多么与众不同的一天啊! 多么特别的一天啊!
教师回复: x趋于0,cosx的极限是1,所以ln(cosx)=ln(1-1+cosx),等价无穷小为-1+cosx,也就是等价无穷小为-1/2 x^2