

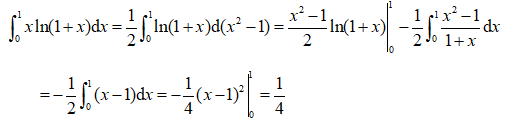
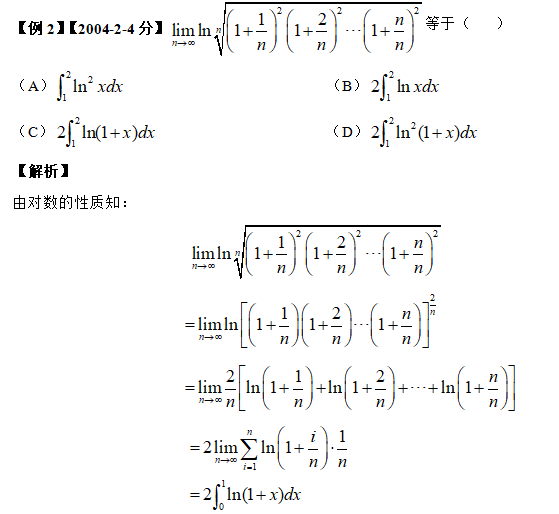


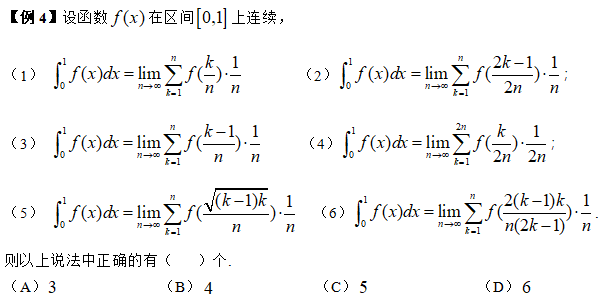




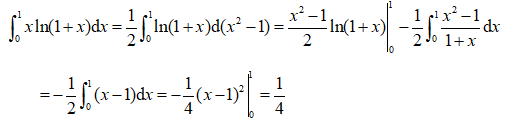
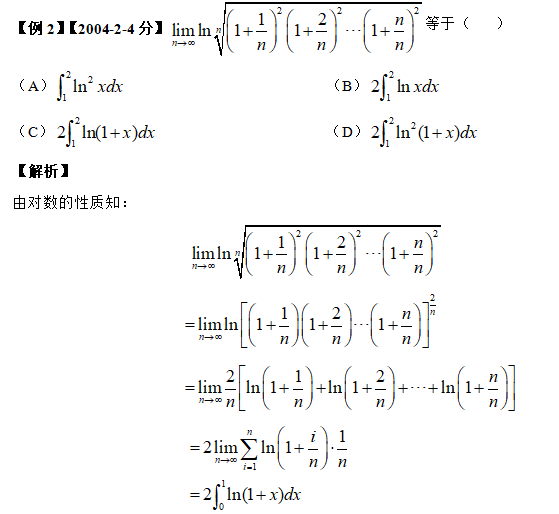


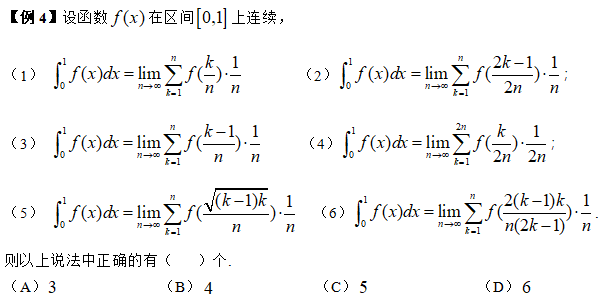


1、凡本网站注明“来源高顿教育”或“来源高顿网校”或“来源高顿”,的所有作品,均为本网站合法拥有版权的作品,未经本网站授权,任何媒体、网站、个人不得转载、链接、转帖或以其他方式使用。
2、经本网站合法授权的,应在授权范围内使用,且使用时必须注明“来源高顿网校”或“来源高顿”,并不得对作品中出现的“高顿”字样进行删减、替换等。违反上述声明者,本网站将依法追究其法律责任。
3、本网站的部分资料转载自互联网,均尽力标明作者和出处。本网站转载的目的在于传递更多信息,并不意味着赞同其观点或证实其描述,本网站不对其真实性负责。
4、如您认为本网站刊载作品涉及版权等问题,请与本网站联系(邮箱fawu@gaodun.com,电话:021-31587497),本网站核实确认后会尽快予以处理。
对于理工科和经管类学生来说,数学必过的一道坎,每年都会有部分考生因为数学拉分,以失败告终。所以掌握数学很重要。下面上海高顿考研网给大家分...
2022-07-06考研数学怎么学都学不会,做一题错一题,数学真的很难吗?面对考研数学不少同学会有这样的疑问,其实数学掌握窍门很重要,下面上海高顿考研网就来...
2022-07-05对于理工科和经管类学生来说,数学必过的一道坎,每年都会有部分考生因为数学拉分,以失败告终。所以掌握数学很重要。下面上海高顿考研网给大家分...
2022-07-05对于理工科和经管类学生来说,数学必过的一道坎,每年都会有部分考生因为数学拉分,以失败告终。所以掌握数学很重要。下面上海高顿考研网给大家分...
2022-07-01如果考研选择的专业需要考高等数学,那你一定要认真准备,因为数学是很容易拉开分数的科目,如果你觉得高数很难,上海高顿考研网告诉你应该怎么去...
2022-06-21考研报考理学的同学,不少不会选择数学,数学下有很多二级学科,考生比较关心研究生毕业后的就业方向,今天上海高顿考研网给大家分析下理学下数学...
2022-06-13理学有一级学科和二级学科之分,它是自然科学、应用科学以及数理逻辑的统称,上海高顿考研网将给大家详细介绍下理学一级学科物理学下的相关学科。...
2022-06-13理学有一级学科和二级学科之分,它是自然科学、应用科学以及数理逻辑的统称,上海高顿考研网将给大家详细介绍下理学一级学科数学下的相关学科,...
2022-06-13老师 为什么第二题不做处理呢 不应该计入资本公积—股本溢价吗
老师好,这道题的会计分录应该是这样的吧,但是我不理解其他综合收益2000那个步骤,他不是以摊余成本计量的金融资产已确认损失2000万吗?不应该是信用减值损失的科目吗?为什么写其他综合收益这个科目在这里?
老师您好,固定资产清理,卖掉时候,转银行存款和资产处置损益,差别在哪里呢。我觉得卖掉固定资产,转哪个都差不多啊,谢谢老师。
选项c,资本公积—股本溢价4500为什么不选?
复旦大学是国家“双一流”、“985工程”、“211工程”建设高校,是一所国内顶尖的综合性研究型大学。该校数学专业是不是双一流学科呢?下面上海高顿考研网就来跟大家介绍一下上海复旦大学双一流建设学科有哪些。...
2022-04-14数学是很多考研专业中的必考科目,但是数学又分数学一/二/三,对于第一次考研的小小伙伴对这些并不是很清晰,下面上海高顿考研网整理了考研数学一/二/三初试考试题型及分值区别,考生可以拿去收藏区别。...
2022-04-07最近有不少23考研的小伙伴来咨询一些上海师范大学对数理学院考研的相关内容,包括参考书、考试科目、拟招人数、复试考试形式及内容等,下面上海高顿考研网为大家整理了上海师范大学数理学院各个学科2022年硕士研究生招生专业目录,供大家参考。...
2022-04-01时光过得很快,复习的时间总是在不经意间从我们的指尖流逝,转眼已经到了2022年3月中旬,国家线、院校复试分数线陆陆续续出炉,23考研数学的复习也越来越紧迫。下面上海高顿考研网将给大家分享一些考研数学定积分定义求极限的方法,包括示例和解析等等。...
2022-03-18学习过线性代数的同学,在学习到矩阵运算这一节的时候,一定看到过矩阵乘法的运算规则,今天上海高顿考研网老师就带你从解方程组的角度,来理解一下这个看起来莫名其妙的运算规则。...
2022-03-18初数到底考什么?对于刚刚接触管综考试的同学来说,初数可能是个还有些陌生的概念。初等数学是不是就等于小初高学的数学?下面上海高顿考研网就来一起跟大家看下初数各章节内容特点。...
2022-03-07学霸能一学就十几个小时不是因为精力旺盛,而是因为学霸适应并沉浸入学习这种状态。那么你为什么不能适应这种状态?那是因为你对考研数学没有找到强烈的刺激点,学习意义。怎样学好数学,跟着上海高顿考研一起来看看吧!...
2022-01-282022年硕士研究生入学考试初试早已落下帷幕,从22考研数学的考题难度和知识点分布来看,有以下四点问题是2023考生在复习过程中需要注意的,跟着上海高顿考研一起来看看吧!...
2022-01-26